Fachkonzept - Asymmetrisches Chiffriersystem
Ein System mit öffentlichem und privatem Schlüssel
Ein asymmetrisches Chiffriersystem ist ein System zum Ver- und Entschlüsseln von Nachrichten, bei dem ein öffentlich bereitgestellter Schlüssel (public key) zum Verschlüsseln und ein privater Schlüssel (private key) zum Entschlüsseln benutzt wird.
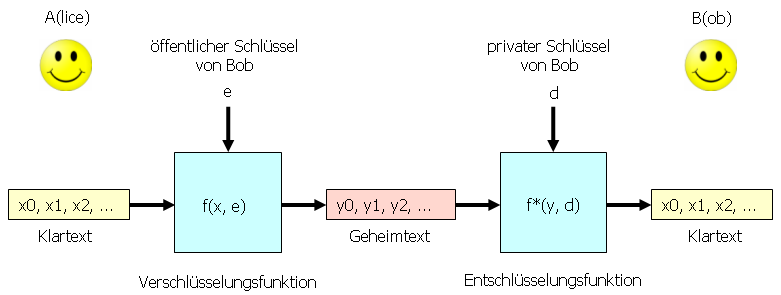
Schlüsselaustausch durch Veröffentlichung des öffentlichen Schlüssels
Der öffentliche Schlüssel wird - wie der Name es sagt - veröffentlicht, so dass jede Zugriff auf diesen Schlüssel hat. Der private Schlüssel bleibt bei seiner Besitzer:in. Diese muss dafür Sorge tragen, dass niemand - außer der Besitzer:in selbst - Zugriff auf diesen Schlüssel hat. Denn, wer im Besitz des privaten Schlüssels ist, kann die mit dem öffentlichen Schlüssel erzeugten Nachrichten entschlüsseln.
Der Schlüsselaustausch ist bei asymmetrischen Chiffriersystemen unproblematisch. Die Besitzer:in eines Schlüsselpaares kann ihren öffentlichen Schlüssel an alle Personen weitergeben, die ihr verschlüsselte Nachrichten zukommen lassen sollen. Die Besitzer:in kann sogar den öffentlichen Schlüssel öffentlich bekannt machen, so dass jede ihn benutzen kann. Erhält die Besitzer:in des öffentlichen Schlüssels eine hiermit verschlüsselte Nachricht, so kann nur sie sie mit ihrem privaten Schlüssel entschlüsseln. Die Inhaber:inn des Schlüsselpaares kann sich aber nicht sicher sein, dass die Person, die sich als Absender:in angibt, tatsächlich diese Person auch ist (vgl. Sicherheitsziele).
Ein Schlüsselpaar für jede Kommunikationsteilnehmer:in
Wenn mehrere Personen verschlüsselte Nachrichten austauschen wollen, dann reicht es, wenn jede Person ein Schlüsselpaar aus öffentlichem und privatem Schlüssel besitzt.
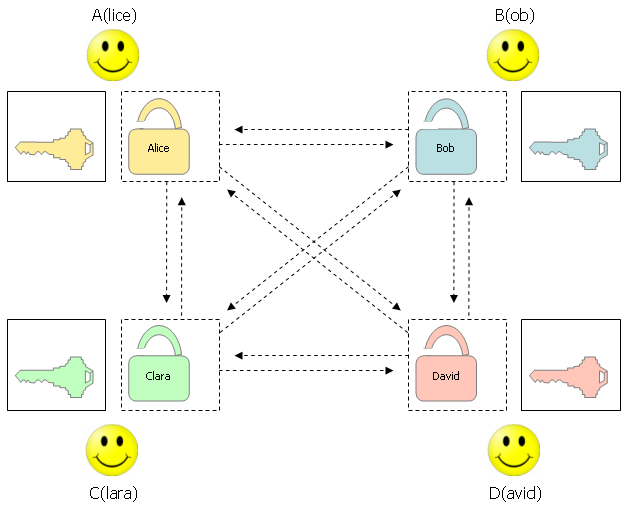
Bei 4 Personen A(lice), B(ob), C(lara) und D(avid), die alle miteinander kommunizieren wollen, werden somit 4 Schlüsselpaare benötigt. Bei n Personen benötigt man entsprechend genau n Schlüsselpaare. Es werden also viel weniger Schlüssel benötigt als bei symmetrischen Chiffriersystemen.
Die Rolle von Einwegfunktionen
Damit so ein Verfahren funktioniert, muss Folgendes gelten:
- Mithilfe der öffentlich verfügbaren Informationen (insbesondere dem öffentlichen Schlüssel $e$) muss es in sinnvoller Zeit möglich sein, den Klartext zum Geheimtext zu verschlüsseln. Außerdem muss es mit dem privaten Schlüssel $d$ in sinnvoller Zeit möglich sein, den Geheimtext zu entschlüsseln. Ansonsten könnte man das Verfahren nie anwenden.
- Mithilfe der öffentlich verfügbaren Informationen darf es – ohne den privaten Schlüssel $d$ – nicht in sinnvoller Zeit möglich sein, den Geheimtext zu knacken, also den Klartext zu rekonstruieren. Daraus folgt, dass auch der private Schlüssel $d$ nicht mithilfe der öffentlichen Informationen in sinnvoller Zeit berechnet werden kann.
Asymmetrische Chiffriersysteme nutzen Funktionen mit den oben dargestellten Eigenschaften – sogenannte Einwegfunktionen. In eine Richtung lassen sie sich in sinnvoller Zeit berechnen, aber die Umkehrung ist – ohne den privaten Schlüssel als Hilfsmittel – kaum möglich.
Auf den ersten Blick klingt es verwunderlich, dass hier immer von „in sinnvoller Zeit“ die Rede ist. Das liegt daran, dass man ja z.B. alle möglichen privaten Schlüssel durchprobieren könnte. Es ist also nicht möglich, das Knacken ganz auszuschließen. Aber, wenn es mit aller Rechenleistung der Welt viele Hundert Millionen Jahre dauern würde, gilt das als ausreichend sicher.
Ein konkretes asymmetrisches Chiffriersystem
In Kapitel Das RSA-Verfahren wird ausführlich ein Verfahren entwickelt, mit dem man ein asymmetrisches Chiffriersystem realisieren kann. Die Grundidee dahinter – insbesondere, welche Einwegfunktion hier verwendet wird, wird im nächsten Abschnitt Ein Einblick ins RSA-Verfahren erarbeitet.

