Verschlüsselung Hinweg
Verschlüsselung nach dem Zwiebelprinzip
Alice möchte über das Tor-Netz eine Nachricht an Bob senden. Dazu wählt sie zunächst zufällig drei Onion-Router X, Y, Z (also drei Rechner des Tor-Netzes) aus, über die die Nachricht nach dem folgenden Schema versandt werden soll: $$ A \rightarrow X\rightarrow Y\rightarrow Z\rightarrow B $$ Jeder der Torknoten X, Y, Z besitzt ein asymmetrisches Schlüsselpaar, hier bezeichnet mit: $$ k_X^{öff, pr}, k_Y^{öff, pr}, k_Z^{öff, pr}$$ Alice möchte nun die Nachricht "Halli" an Bob senden. Sie verwendet dazu im Folgenden das Schema $$\lt Empfängerin \gt : \lt Inhalt \gt,$$ um jeweils die Empfängerin und den Inhalt eine Nachricht zu kodieren: Nun startet Alice damit, ihre Nachricht sukzessive zu verschlüsseln. Im ersten Schritt verschlüsselt Sie ihre Nachricht zunächst mit dem öffentlichen Schlüssel von Z: $$k_Z^{öff}(''B:Halli'')$$ Dieser Geheimtext soll später an Z gesendet werden, deshalb stellt Alice ihm nach dem oben eingeführten Schema noch die Empfängerin Z voran und verschlüsselt das Ergebnis anschließend mit dem öffentlichen Schlüssel von Y: $$k_Y^{öff}(Z:k_Z^{öff}(''B:Halli'')))$$ Der so entstehende Geheimtext soll später an Y geschickt werden, also stellt Alice wiederum die Empfängerin voran und verschlüsselt im letzten Schritt mit dem öffentlichen Schlüssel von X: $$ k_X^{öff}(Y:k_Y^{öff}(Z:k_Z^{öff}(''B:Halli'')))$$Mit dem bereits vorher benutzen Bild von Briefumschlägen lässt sich die sukzessive Verschlüsselung darstellen als:
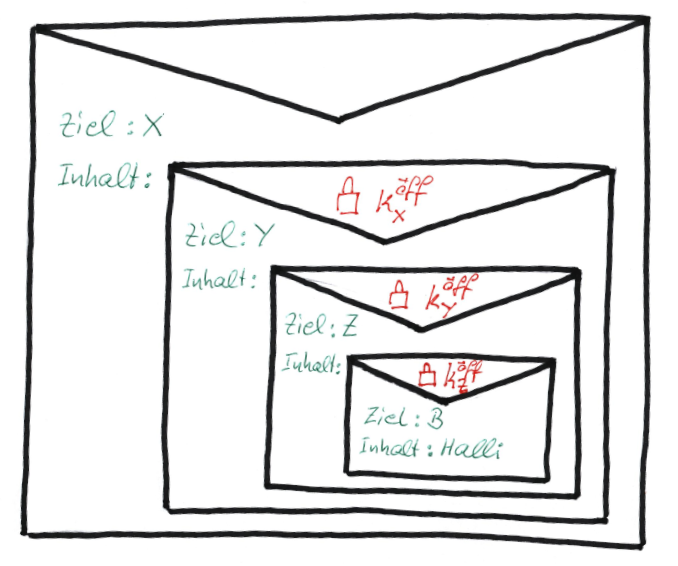
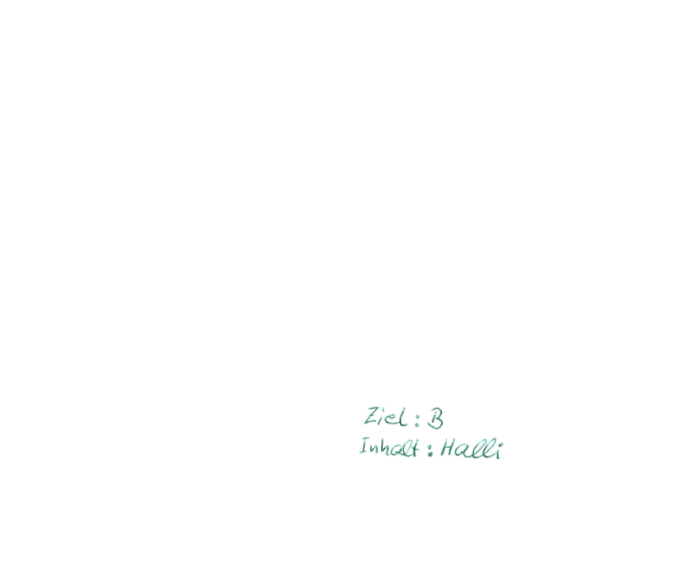



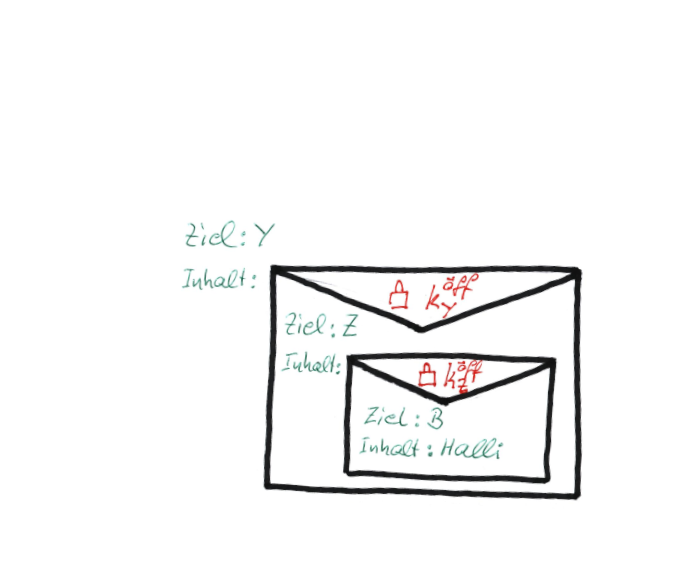
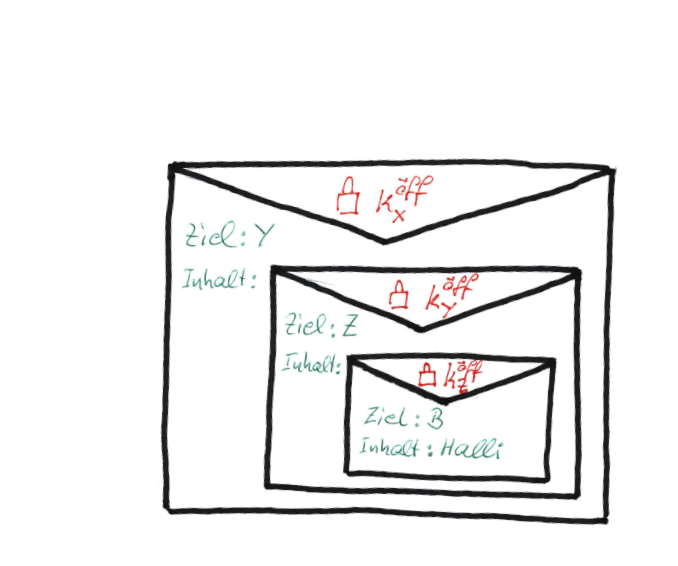
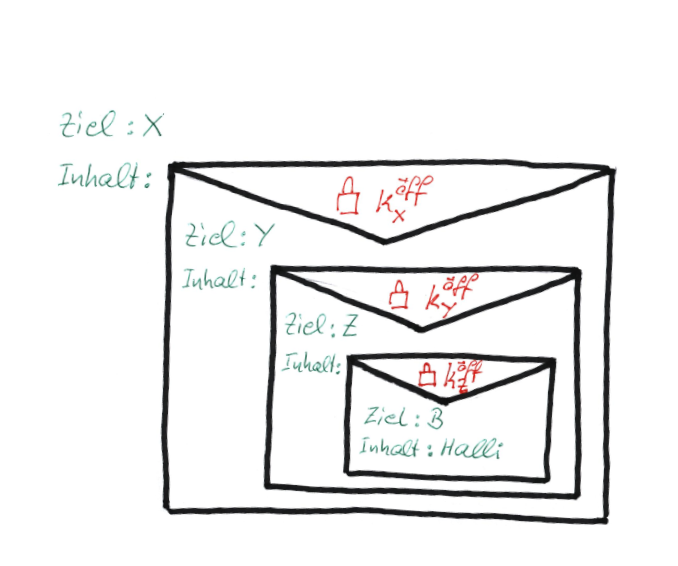

Absenden der "Verschüsselungs-Zwiebel"
Nun sendet Alice diesen Geheimtext aus dem letzten Schritt an X. Diese erhält also das folgende Datenpaket $$ X:k_X^{öff}(Y:k_Y^{öff}(Z:k_Z^{öff}(''B:Halli''))).$$ Da X im Besitz des privaten Schlüssels $k_X^{pr}$ ist, kann sie die äußere Verschlüsselungsschicht entfernen und erhält das Datenpaket $$ Y:k_Y^{öff}(Z:k_Z^{öff}(''B:Halli'')).$$ Von diesem kann X im Klartext allerdings lediglich erkennen, dass es weiter an die Empfängerin Y gehen soll. Den Inhalt des Datenpakets kann X aufgrund der Verschlüsselung nicht lesen. Ebenso wenig kann sie erkennen, dass das Datenpaket anschließend weiter zu Z oder gar zu Bob gesendet werden soll.Nachdem X das Paket also weiter an Y geschickt hat, entfernt Y wiederum eine Verschlüsselungsschicht und erhält so das Paket: $$Z:k_Z^{öff}(''B:Halli'').$$
Beachte hier wiederum, dass Y keine Kenntnis von der ursprünglichen Absenderin Alice oder gar dem endgültigen Empfänger Bob erlangt. Sie erkennt lediglich, dass das Paket an Z weiter geschickt werden soll. Z wiederum entfernt mit ihrem privaten Schlüssel die letzte Verschlüsselungsschicht und erhält damit die Nachricht
$$''B:Halli''.$$ Diese Nachricht sendet Z nun weiter an Bob. Beachte, dass Z der Exitknoten ist. Die Nachricht an Bob verlässt also hier das Tor-Netz und wird über das herkömmliche Internet an Bob gesendet. Falls dazu das Protokoll https genutzt wird, wird die Nachricht dabei mit einer Transportverschlüsselung versehen. Im Fall von http wird sie allerdings auf dem Weg vom Exitknoten zum endgültigen Empfänger unverschlüsselt übertragen.
