Separationsgerade

Wir bleiben bei dem oben gewählten Perzeptron mit zwei Eingängen zur Klassifikation von Tieren nach ihrer Gefährlichkeit: 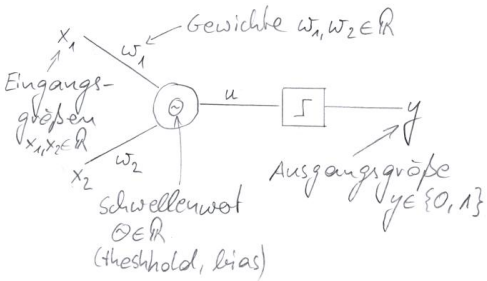Punkte in der 2-dimensionalen Zahlenebene können als Tiere aufgefasst werden. Die Punktmenge $(x_1,x_2)$, für die $u(x_1,x_2)=\Theta$ gilt, separiert gefährliche von ungefährlichen Tieren: \begin{eqnarray} u(x_1,x_2) &\stackrel{!}{=}& \Theta \nonumber \\ \Leftrightarrow w_1 x_1 + w_2 x_2 &=& \Theta \nonumber \\ \Leftrightarrow \vec{w} \cdot \vec{x} - \Theta &=& 0 \label{eq:gerade} \end{eqnarray} Dies ist eine Geradengleichung, die nach Division durch $\|\vec{w}\|$ mit dem Einheitsvektor $\vec{\hat{w}} := \frac{\vec{w}}{\|\vec{w}\|} $ in der Hesseschen Normalenform geschrieben werden kann als: \begin{eqnarray} \Leftrightarrow \hat{\vec{w}} \cdot \vec{x} - \frac{\Theta}{\|\vec{w}\|} &=& 0 \nonumber \nonumber \end{eqnarray} Aus der Hesseschen Normalenform wiederum erhält man den vorzeichenbehafteten Abstand eines Punktes $P$ mit Ortsvektor $\vec{p}$ von der Separationsgerade $g$ als \begin{eqnarray} d(\vec{p},g) = \vec{w} \cdot \vec{p} - \Theta \nonumber \end{eqnarray} Dabei ist $d(\vec{p},g)$ positiv, wenn P in dem durch die Gerade getrennten Halbraum liegt, in den der Gewichtsvektor $\vec{w}$ hineinzeigt und negativ, wenn $P$ in dem anderen Halbraum liegt. Weiterhin benötigen wir im Folgenden die Geradengleichung von $g$ auch noch in der Koordinatenform, die wir durch Ausmultiplizieren des Skalarproduktes erhalten als: \begin{eqnarray} \Leftrightarrow \frac{w_1}{\Theta} x_1 + \frac{w_2}{\Theta} x_2 &=& 1 \nonumber \end{eqnarray} Aus der Koordinatengleichung erhält man für die Schnittpunkte mit den Koordinatenachsen also $(\frac{\Theta}{w_1},0)$ und $(0,\frac{\Theta}{w_2})$.

Der Abstand der Separationsgeraden von Koordinatenursprung beträgt $d=\frac{\Theta}{\|\vec{w}\|}$, wie man aus der HNF abliest. Damit läßt sich die allgemeine Separationsgerade wie folgt graphisch darstellen:

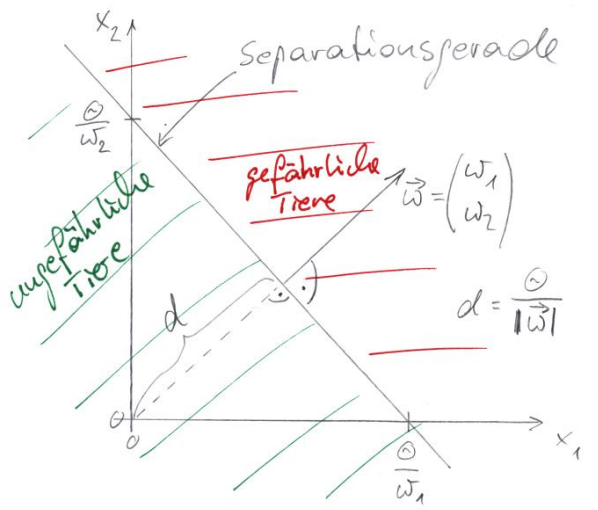Die Gerade trennt den Bereich der ungefährlichen Tieren von dem Bereich der gefährlichen Tiere. Der Verktor $\vec{w}$ zeigt in den Halbraum, für den das Perzeptron aktiviert ($y=1$) ist, also hier in den Bereich der gefährlichen Tiere.

Aufgabe 1:

Stelle für das obige Perzeptron zur Klassifikation von Tieren ($w_1=1, w_2=0,5,\Theta=2$) die Separationsgerade graphisch in der Zahlenebene dar.

Aufgabe 2:

Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert $y=1$, für die grün eingezeichneten Punkte den Wert $y=0$ annehmen.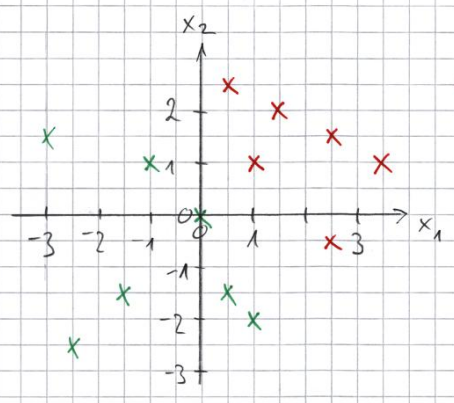

Aufgabe 3:

Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert $y=1$, für die grün eingezeichneten Punkte den Wert $y=0$ annehmen.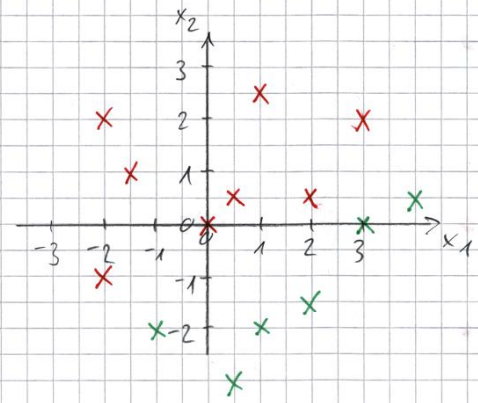

Aufgabe 4:

Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das eine AND-Verknüpfung modelliert, indem es die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert TRUE ($y=1$), für die grün eingezeichneten Punkte den Wert FALSE ($y=0$) annehmen.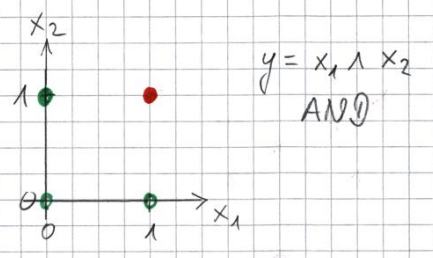

Aufgabe 5:

Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das eine NAND-Verknüpfung modelliert, indem es die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert TRUE ($y=1$), für die grün eingezeichneten Punkte den Wert FALSE ($y=0$) annehmen.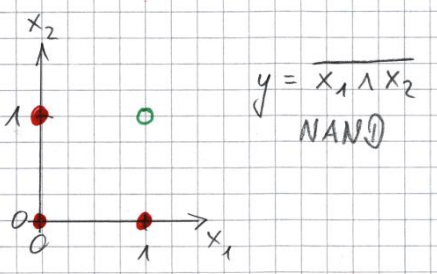

Aufgabe 6:

Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das eine OR-Verknüpfung modelliert, indem es die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert TRUE ($y=1$), für die grün eingezeichneten Punkte den Wert FALSE ($y=0$) annehmen.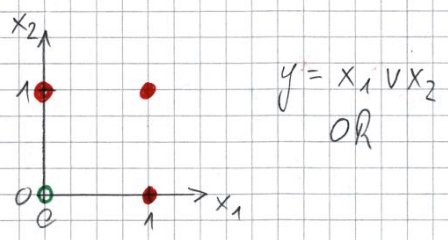

Aufgabe 7:

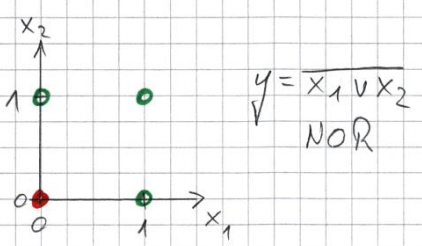
Finde Gewichte $w_1,w_2 \in \mathbb{R}$ und Schwellenwert $\Theta \in \mathbb{R}$ eines Perzeptrons, das eine NOR-Verknüpfung modelliert, indem es die folgende Punktwolke separiert. Für die rot eingezeichneten Punkte soll der Ausgang des Perzeptrons den Wert TRUE ($y=1$), für die grün eingezeichneten Punkte den Wert FALSE ($y=0$) annehmen.