Mehrlagige Perzeptrone

Ein mehrlagiges Perzeptron besteht aus mehreren Neuronen. Diese sind in Schichten (oder Lagen, engl. Layer) angeordnet. Die Ausgänge einer Schicht dienen als Eingänge der nächsten Schicht. Wir werden in dieser Darstellung die einzelnen Lagen von Neuronen mit $A,B,C$ usw. durchnummerieren, wobei wir uns zunächst mit zwei Neuronenschichten ($A$ und $B$) begnügen.

Bei allen Zahlengrößen, die Neuronen einer bestimmten Schicht betreffen, werden wir die Lage hinter der Größe hochgestellt in Klammern hinschreiben, um Verwechslungen zu vermeiden. Das sieht zunächst vielleicht ein bisschen kompliziert aus, ist aber tatsächlich nur eine kleine Markierung. Beispiel: $$y_2^{(A)}$$ beschreibt den Ausgang des 2. Neurons in Schicht $A$.

Wir betrachten den (typischen) Fall, das jedes Neuron einer Schicht mit jedem Neuron der nächsten Schicht über eine Synapse verbunden sind.

Beim einfachen Perzeptron mit nur einem Neuron war es nur nötig, die Eingänge zu nummerieren. Beim mehrlagigen Perzeptron sind die Eingänge des Gesamtnetzes sowie die einzelnen Neuronen einer Schicht durchnummeriert. Bei der allgemeinen Schreibweise werden wir die die Nummer der Eingänge mit $i$, die Nummer der Neuronen der Schicht $A$ mit $j$ und die Neuronen der Schicht $B$ mit $k$ durchnummerieren. Wobei wir zunächst wieder eine Vereinfachung machen, und die Schicht $B$ wieder aus nur einem einzelnen Neuron bestehen lassen; $k$ kann also nur den Wert $1$ annehmen.

Wir betrachten den (typischen) Fall, das jedes Neuron einer Schicht mit jedem Neuron der nächsten Schicht über eine Synapse verbunden ist und jeder Eingang über eine Synapse mit jedem Neuron von Schicht $A$.

$$x_j^{(B)}=y_j^{(A)}$$

Für die Synapsen, die die Eingänge mit Schicht $A$ verbinden, schreiben verwenden wir das Formelzeichen $w_{i,j}^{(A)}$: Diese Synapse verbindet den Eingang der Nummer $i$ mit dem Neuron aus Schicht $A$ mit der Nummer $j$. Genauso schreiben wir $w_{j,k}^{(B)}$ für die Synapse, die das $j$-te Neuron aus Schicht $A$ mit dem $k$-ten Neuron aus Schicht $B$ verbindet. Im Fall, dass wir nur ein ein einziges Neuron in der Schicht $B$ betrachten, schreiben wir $w_{j,1}^{(B)}$

Die Neuronen funktionieren ähnlich wie beim Perzeptron. Die Aktivierung $a$ wird genauso berechnet wie vorher: Wenn die Schicht $A$ beispielsweise aus Neuronen mit jeweils 2 variablen und einem konstanten Eingang (also insgesamt drei Eingängen) besteht, berechnet sich für ein Neuron mit Nr. $j$ aus dieser Schicht die Aktivierung mit:

$$a_j^{(A)}=w_{1,j}^{(A)}\cdot x_1^{(A)}+w_{2,j}^{(A)}\cdot x_2^{(A)}+w_{3,j}^{(A)}\cdot x_3^{(A)}$$ Genauso gilt für die Aktivierung eines Neurons aus Schicht $B$: $$\begin{array}{rcl}{a}_k^{(B)}& =& w_{1,k}^{(B)}\cdot x_1^{(B)}+w_{2,k}^{(B)}\cdot x_2^{(B)}+w_{3,k}^{(B)}\cdot x_3^{(B)}\\ & =& w_{1,k}^{(B)}\cdot y_1^{(A)}+w_{2,k}^{(B)}\cdot y_2^{(A)}+w_{3,k}^{(B)}\cdot y_3^{(A)}\end{array}$$

Leicht geändert ist jedoch die Ausgabefunktion: Wir wählen eine Funktion, die nun alle Werte zwischen $-1$ und $+1$ annehmen kann. Für beide Schichten gilt:

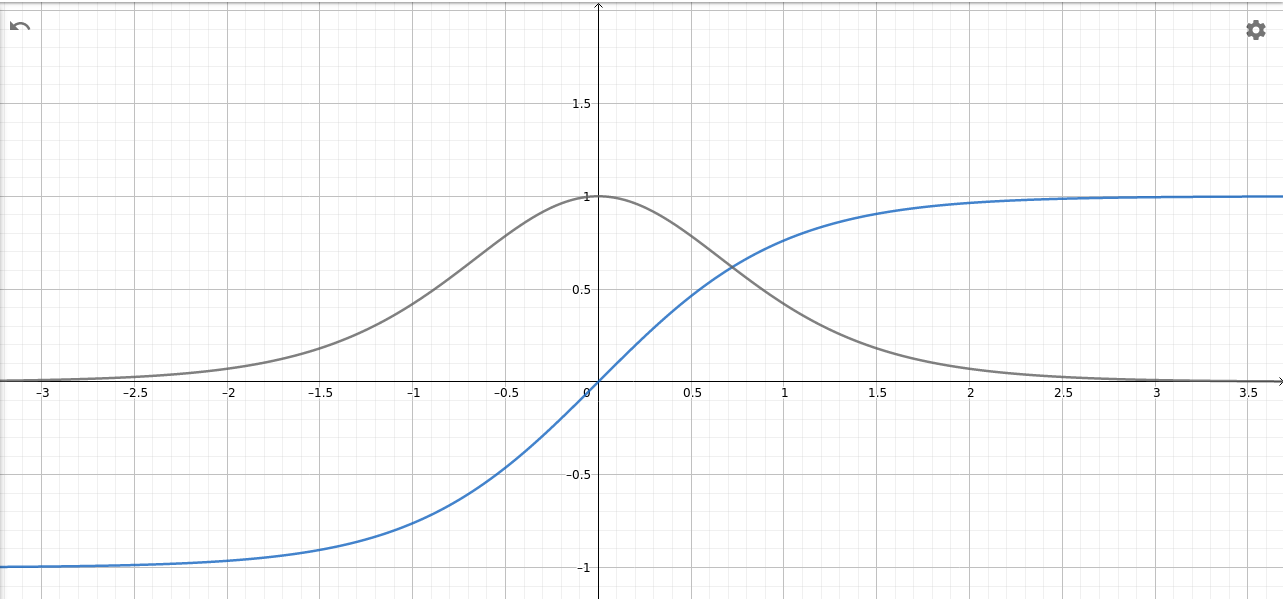
$$y_j=f(a_j)=\tanh (a_j)$$

Gesprochen wird das "Tangens Hyperbolicus von $a_j$". Allerdings darf man sich wegen des schwierigen Namens nichts besonders Kompliziertes (oder gar "Magisches") vorstellen. Man hat eine mathematische Funktion gesucht, die für sehr stark negative Werte von $a$ einen Wert nahe $-1$ liefert und nur wenige ansteigt. Für sehr große positive Werte soll sie einen Wert nahe $+1$ liefern und ebenfalls sehr wenig ansteigen. Den stärksten Anstieg soll sie für $a=0$ haben, also sozusagen "in der Mitte".

Die Tangens-Hyperbolicus-Funktion ist nun eine Funktion mit genau diesen Eigenschaften, die man am einfachsten hinschreiben kann: Python hat im Modul math die Funktion bereits vordefiniert. Jede andere Funktion mit ähnlichen Eigenschaften würde genauso funktionieren.

Die "Steilheit" der Funktion an den verschiedenen Stellen (mathematisch: die "Ableitung") dieser Funktion wird bezeichnet als $$f^{\prime }(a_j)=-\tanh (a_j{)}^2+1$$ Diese nimmt für sehr große und sehr kleine Werte von $a_j$ einen Wert nahe 0 an, für $a_j=0$ nimmt sie den Wert $1$ an, um $a_j=0$ herum steigt sie zunächst an und fällt dann wieder ab.