Einstieg Halbaddierer
Das Prinzip Modularisierung
Das Prinzip der Modularisierung bietet einen flexiblen, dynamischen Ansatz. Modularisierung kennst du schon aus anderen Kapiteln wie Konzepte imperativer Programmierungoder Objektorientierte Programmierung mit Python.
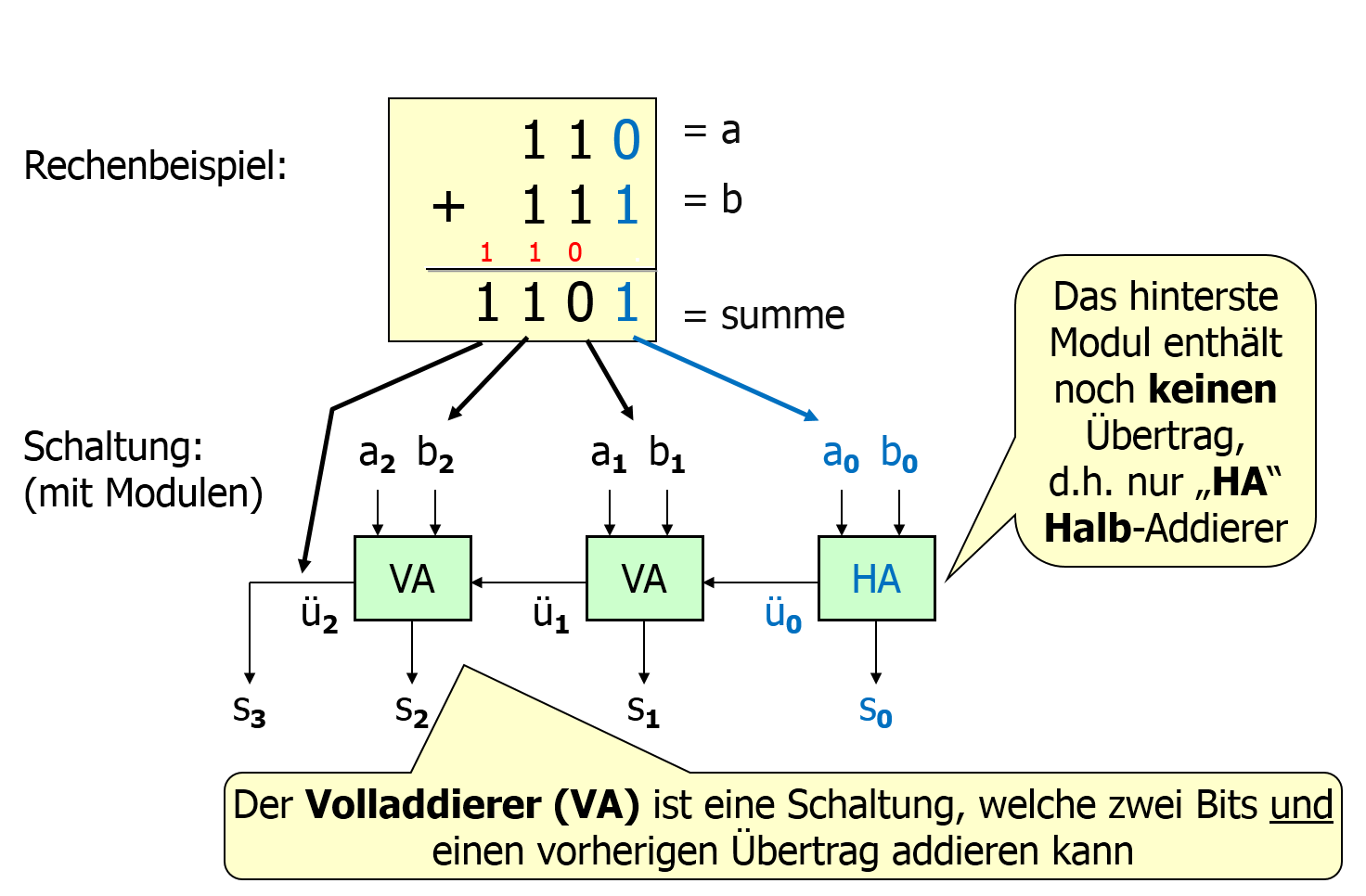
Kommen wir auf das zuvor kennen gelernte Beispiel zurück. Sicherlich hast du bemerkt, dass das hintere Modul (blau markiert) keinen Übertrag
als Eingang enthält, sondern nur die beiden niederwertigsten Bits a0 und b0 der Dualzahlen a und b. Solche Module, die genau zwei einstellige
Dualzahlen addieren, nennt man Halbaddierer.
Module, die neben zwei einstelligen Dualzahlen noch einen möglichen Übertrag der vorherigen Stelle addieren, nennt man
Volladdierer. Diesen wirst du ein
Kapitelweiter kennenlernen.
Halbaddierer
Ziel soll es nun sein, einen solchen Halbaddierer zu entwickeln.
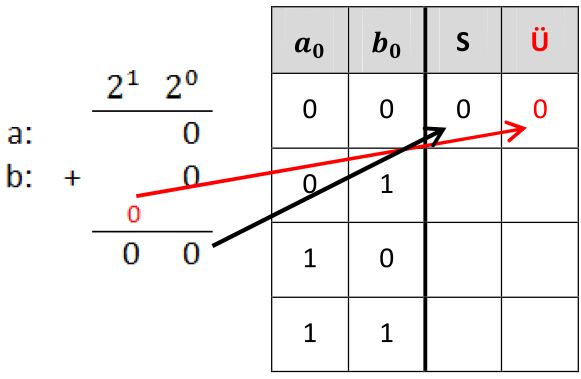
Zunächst addieren wir zwei Zahlen a0 und b0 der Länge 1 - also einstellige Zahlen. Beachte, dass neben der Summe S auch ein Übertrag Ü entstehen kann.
Aufgabe 1
(a) Notiere die Rechnungen für die weiteren Kombinationen für a0 und b0 und ergänze damit die Wahrheitstabelle.
(b) Betrachte die Ausgangsspalten S und Ü. Welchem der 6 kennengelernten Gatterentspricht Ausgang S, welchem Ü?
(c) Entwickle für die einstellige Addition die zugehörige Schaltung als Modulbaustein, benenne ihn mit Halbaddierer (HA) und teste diesen. Nutze dafür LogicSim (siehe Kapitel Module mit LogicSim) oder DSimWeb (nachfolgende Simulation; Anleitung auf Seite Module mit DSimWeb).
Aufgabe 2
Halte deine Erkenntnisse zum Halbaddierer in diesem Wissensspeicher fest. Du wirst ihn später noch um einen sogenannten Volladdierer erweitern.
Quellen
- [1]: - Urheber: SD - Lizenz: inf-schule.de
- [2]: - Urheber: SD - Lizenz: inf-schule.de