XOR-Problem
Die sogennante XOR-Funktion $y=x_1 \underline{\lor} x_2 = (x_1 \land \overline{x}_2 ) \lor (\overline{x}_1 \land x_2)$ ist durch ein einzelnes Perzeptron nicht modellierbar, wie man sofort anhand der folgenden Abbildung erkennen kann:
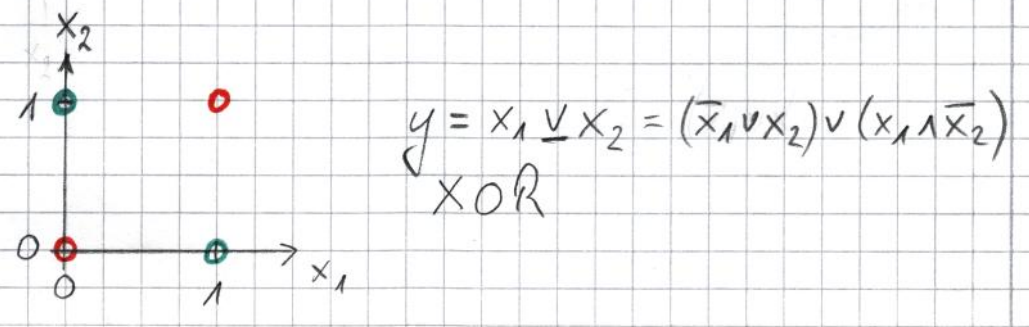
Die grün eingezeichneten Punkte sind von den rot eingezeichneten Punkten nicht durch eine Gerade separierbar, so dass sich die XOR-Funktion nicht mittels eines einzelnen Perzeptrons modellieren lässt.
Das XOR-Problem kann dennoch mittels Perzeptronen beschrieben werden, indem mehrere einzelnen Perzeptronen wie folgt zu einem so genannten künstlichen neuronalen Netz (KNN) zusammengeschaltet werden.
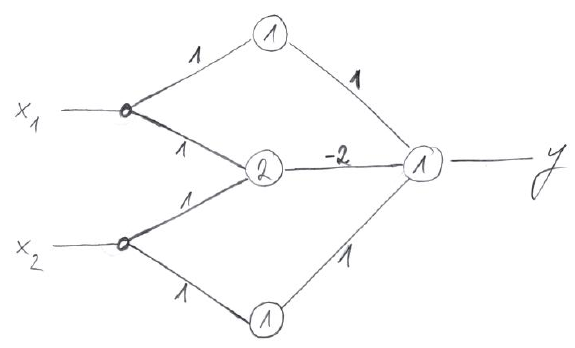
Die Abbildung zeigt ein künstliches neuronales Netz zur Modellierung der XOR-Funktion $y=x_1 \underline{\lor} x_2$. Beachte, dass die beiden so genannten Eingangsperzeptronen im strengeren Sinne gar keine echten Perzeptronen sind, da sie lediglich ihre Eingangswerte unverändert an die nächste Schicht von Perzeptronen weiterleiten.
Die Ausgänge der beiden so genannten Eingangsperzeptronen leiten dabei die an ihren Eingängen anliegenden Werte $x_1$ bzw. $x_2$ unverändert weiter an die Eingänge dreier Perzeptronen in einer verborgenen Schicht, einem so genannten hidden layer. Die Ausgänge der Perzeptronen des hidden layers wiederum stellen die drei Eingänge des Ausgabeperzeptrons dar.
Durch Ausprobieren aller vier möglichen Eingangkonfigurationen stellt man fest, dass dieses KNN das XOR-Problem löst, dass also gilt:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nachdem Rosenblatt 1958 seinen Lernalgorithmus für ein einzelnes Perzeptron veröffentlicht hatte, bestand zunächst ein großes Interesse an Forschung auf dem Gebiet der künstlichen Intelligenz (KI). Allerdings konnte der Lernalgorithmus damals noch nicht auf künstliche neuronale Netze verallgemeinert werden, welche aus einer Vielzahl einzelner Perzeptronen zusammengesetzt sind. Infolgedessen ebte das Interesse an künstlicher Intelligenz nach und nach ab und es kam zum so genannten KI-Winter.
Erst 1986 gelang es Rumelhard, Hinton und Williams mit ihrem so genannten Backpropagation-Algorithmus die Lernregel von Rosenblatt auf künstliche neuronale Netze zu verallgemeinern. Gleichzeitig wurden immer leistungsfähigere Computer entwickelt, so dass es nun möglich wurde, immer größere künstliche neuronale Nezte mit Hilfe von Trainigsdaten automatisiert maschinell lernen zu lassen. Damit wurde allmählich das Ende des KI-Winters eingeleitet und es kam zu einem erneuten starken Interesse an Forschung auf dem Gebiet der KI, welches bis heute anhält.
Aktuell ist sogar ein regelrechter Hype auf dem Gebiet der künstlichen Intelligenz zu beobachten, so dass teilweise sogar versucht wird, KI-Verfahren auf Probleme anzuwenden, für die sie als Werkzeug überhaupt nicht geeignet sind. Daraus ergeben sich dann zum Teil erhebliche moralische und ethische Fragen und Probleme, auf die im weiteren Verlauf des Kapitels noch genauer eingegangen wird.
Aufgabe 1:
Modelliere die Funktion $y=\overline{x_1 \underline{\lor} x_2} = (x_1 \land x_2 ) \lor (\overline{x}_1 \land \overline{x}_2)$, also| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
