Separationsgerade
Wir bleiben bei dem oben gewählten Perzeptron mit zwei Eingängen zur Klassifikation von Tieren nach ihrer Gefährlichkeit, allerdings nun mit beliebigen reellen Größen und Parametern:
$$
\begin{eqnarray}
\text{Eingangsgrößen} &:& \quad x_1, x_2 \in \mathbb{R} \\
\text{Gewichte} &:& \quad w_1, w_2 \in \mathbb{R} \\
\text{Schwellenwert} &:& \quad \Theta \in \mathbb{R} \\
\text{Ausgangsgröße} &:& \quad y \in \mathbb{R}
\end{eqnarray}
$$
Punkte in der 2-dimensionalen Zahlenebene können als Tiere aufgefasst werden. Die Punktmenge $(x_1,x_2)$, für die die Bedingung $u(x_1,x_2)=\Theta$ gilt, separiert gefährliche von ungefährlichen Tieren:
\begin{eqnarray}
u(x_1,x_2) &\stackrel{!}{=}& \Theta \nonumber \\
\Leftrightarrow w_1 x_1 + w_2 x_2 &=& \Theta \nonumber \\
\Leftrightarrow \vec{w} \cdot \vec{x} - \Theta &=& 0 \label{eq:gerade}
\end{eqnarray}
Dies ist eine Geradengleichung, die nach Division durch $\|\vec{w}\|$ mit dem Einheitsvektor $\vec{\hat{w}} := \frac{\vec{w}}{\|\vec{w}\|} $ in der Hesseschen Normalenform geschrieben werden kann als:
\begin{eqnarray}
\Leftrightarrow \hat{\vec{w}} \cdot \vec{x} - \frac{\Theta}{\|\vec{w}\|} &=& 0 \nonumber \nonumber
\end{eqnarray}
Aus der Hesseschen Normalenform wiederum erhält man den vorzeichenbehafteten Abstand eines Punktes $P$ mit Ortsvektor $\vec{p}$ von der Separationsgerade $g$
als
\begin{eqnarray}
d(\vec{p},g) = \vec{w} \cdot \vec{p} - \Theta \nonumber
\end{eqnarray}
Dabei ist $d(\vec{p},g)$ positiv, wenn P in dem durch die Gerade getrennten Halbraum liegt, in den der Gewichtsvektor $\vec{w}$ hineinzeigt und negativ, wenn $P$ in dem anderen Halbraum liegt.
Weiterhin benötigen wir im Folgenden die Geradengleichung von $g$ auch noch in der Koordinatenform, die wir durch Ausmultiplizieren des Skalarproduktes erhalten als:
\begin{eqnarray}
\Leftrightarrow \frac{w_1}{\Theta} x_1 + \frac{w_2}{\Theta} x_2 &=& 1 \nonumber
\end{eqnarray}
Aus der Koordinatengleichung erhält man für die Schnittpunkte mit den Koordinatenachsen also $(\frac{\Theta}{w_1},0)$ und $(0,\frac{\Theta}{w_2})$.
Der Abstand der Separationsgeraden von Koordinatenursprung beträgt $d=\frac{\Theta}{\|\vec{w}\|}$, wie man aus der Hesseschen Normalenform abliest. Damit läßt sich die allgemeine Separationsgerade wie folgt graphisch darstellen:
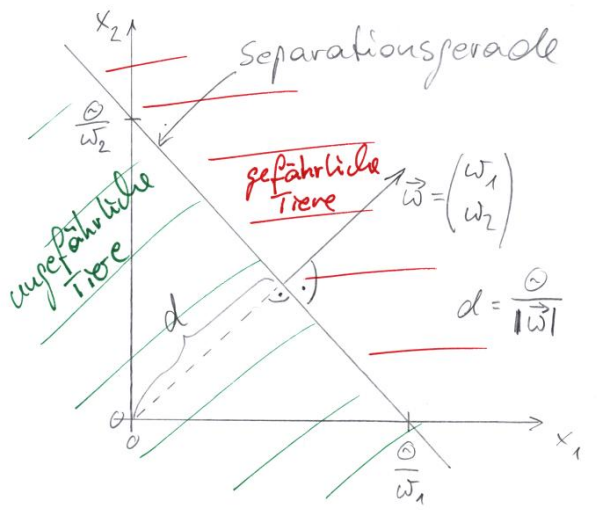
Diese Gerade nennt man Separationsgerade, sie trennt den Bereich der ungefährlichen Tiere von dem Bereich der gefährlichen Tiere. Der Vektor $\vec{w}$ zeigt in den Halbraum, für den das Perzeptron aktiviert ($y=1$) ist, also hier in den Bereich der gefährlichen Tiere.
Das war jetzt eine gute Portion Mathematik. Um in das Thema hineinzufinden und es gut zu durchdringen, gibt es deshalb jetzt einige Übungen, die am besten zunächst einmal "unplugged", also mit Papier und Bleistift durchgeführt werden.
Aufgabe 1
Welche Auswirkungen hätte der Versuch, im Perzeptron auf den Schwellenwert zu verzichten und ausschließlich Gewichte als Prameter zu verwenden?