Station - Korrektheit des Verfahrens

Verfahren mit modularer Potenz

Die Übersicht zeigt anhand eines Beispiels, wie das Verfahren mit modularer Potenz funktioniert.

Zum Verschlüsseln wird hier im Beispiel der öffentliche Schlüssel (e, n) = (13, 77), zum Entschlüsseln der private Schlüssel (d, n) = (37, 77) benutzt.

Die Verschlüsselung einer Zahl x mit einem öffentlichen Schlüssel (e, n) erfolgt mit der Rechnung:

x -> [xe]% n

Die Entschlüsselung einer Zahl y mit einem privaten Schlüssel (d, n) erfolgt analog mit der Rechnung:

y -> [yd]% n

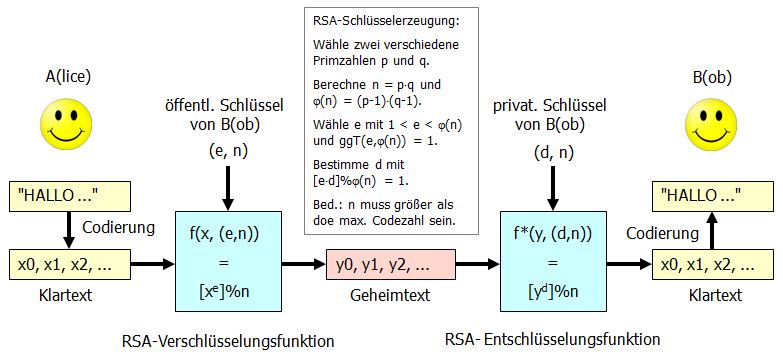
Die folgende Übersicht zeigt das Verfahren einschließlich der Schlüsselerzeugung.

Korrektheit des Verfahrens mit modularer Multiplikation

Korrektheitsüberlegungen liefern auch den entscheidenenden Hinweis, wie öffentlicher und privater Schlüssel bei dem Verfahren mit modularer Multiplikation zusammenhängen.

x
|                          # verschlüsseln
[xe]%n
|                          # entschlüsseln
[([xe]%n)d]%n
|                          # Rechengesetze
[x(e*d)]%n
|                          # ???
x

Zu zeigen ist also die folgende Schlüsseleigenschaft:

[x(e*d)]%n = x für alle Zahlen x < n

Mathematische Herleitung

Schritt 1:

Es gilt n = p*q mit zwei verschiedenen Primzahlen p und q. Wir zeigen:

[x(e*d)]%p = [x]%p und [x(e*d)]%q = [x]%q für alle Zahlen x < n

Es reicht, den Nachweise für eine der beiden Primzahlen p und q zu führen. Der Nachweis für die andere Primzahl verläuft dann völlig analog. Wir betrachten im Folgenden die Primzahl p.

Fall 1: p und x sind nicht teilerfremd.

Da p eine Primzahl ist, muss in diesem Fall p ein Teiler von x sein. Die Primzahl p muss dann auch ein Teiler der Potenz x^(e*d) sein. Es folgt:

[x]%p = 0 und [x(e*d)]% p = 0 

Also:

[x(e*d)]%p = [x]%p

Fall 2: p und x sind teilerfremd.

Nach dem kleinen Fermatschen Satz gilt dann:

[x(p-1)]%p = 1

Nach der Konstruktion der Schlüssel gilt:

[e*d]%φ(n) = 1

Da

φ(n) = (p-1)*(q-1),

gibt es also eine Zahl a mit

e*d = a*(p-1)*(q-1)+1.

Jetzt können wir folgende Umformungen vornehmen:

[x(e*d)]%p 
=
[x(a*(p-1)*(q-1)+1)]%p 
=
[x(a*(p-1)*(q-1))*x]%p 
=
[x(a*(p-1)*(q-1))]%p * [x]%p
=
[([x(p-1)]%p)(a*(q-1))]%p * [x]%p
=
[1(a*(q-1))]%p * [x]%p
=
1 * [x]%p
=
[x]%p

Damit ist die Behauptung von Schritt 1 gezeigt.

Schritt 2:

Aus

[x(e*d)]%p = [x]%p und [x(e*d)]%q = [x]%q

(für alle Zahlen x < n) können wir jetzt (mit dem Satz über modulare Gleichheit bzgl. Primzahlen) schließen:

[x(e*d)]%(p*q) = [x]%(p*q)

Wegen n = p*q und x < n gilt dann:

[x(e*d)]%n = x