Station - Sicherheit des Verfahrens

Angriffsszenario

Die folgende Übersicht verdeutlicht ein Angriffszenario auf eine mit dem RSA-Verfahren verschlüsselte Nachricht.

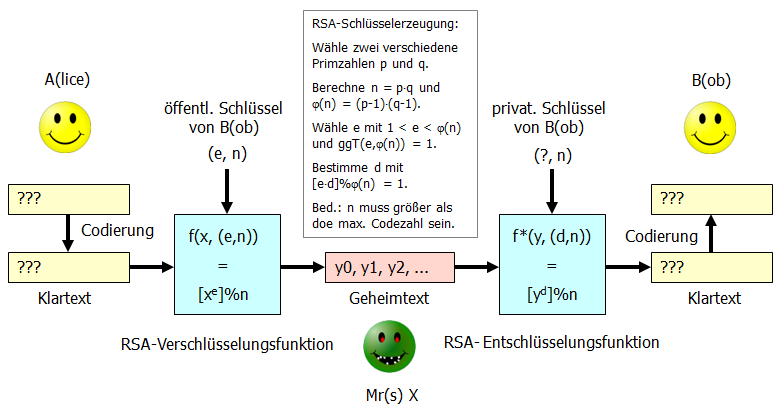
Mr(s). X verfügt neben dem abgefangenen Geheimtext (Sequenz von Zahlen) über eine Reihe weiterer Informationen. Er/Sie kennt den öffentlichen Schlüssel, der zum Verschlüsseln benutzt wurde. Er/Sie kennt zudem alle Details des RSA-Verfahres: benutzte Codierung, Verfahren zur Erzeugung der Schlüssel, Verfahren zum Ver- und Entschlüsseln mit modularer Potenzbildung.

Aufgabe 1

Der öffentliche Schlüssel von Alice ist (19, 65). Es wurde unsere Standardcodierung mit einer Blocklänge 1 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:

[48, 9, 60, 38, 60, 0, 58, 47, 31, 60, 59, 59, 60, 0, 1, 31, 59, 0, 58, 1, 38, 38, 9, 60, 14]

Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln?

Aufgabe 2

Der öffentliche Schlüssel von Alice ist (113, 6887). Es wurde unsere Standardcodierung mit der Blocklänge 2 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:

[6613, 5456, 1378, 2773, 1646, 5581, 4072]

Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln? Wo liegt jetzt das Problem?

Aufgabe 3

Der öffentliche Schlüssel von Alice ist (1432765433173537777777, 1914269284601333234385791628203). Es wurde unsere Standardcodierung mit der Blocklänge 15 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:

[1484723618683282017476932691981, 1335981139459882474539235587779]

Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln? Wo liegt jetzt das Problem?

Angriff auf das RSA-Verfahren

Wenn Mr(s). X über den privaten Schlüssel (d, n) verfügt, kann er/sie den Geheimtext entschlüsseln.

Da n aus dem öffentlichen Schlüssel bekannt ist, muss Mr(s). X nur noch d bestimmen.

Mr(s). X weiß, dass n das Produkt aus zwei verschiedenen Primzahlen ist. Mr(s). X zerlegt also n in ein Produkt p*q mit den beiden Primzahlen p und q.

Beispiel (Aufgabe 1): n = 65 -> p = 5 und q = 13

Aus den beiden Primzahlen p und q kann Mr(s). X die Zahl φ(n) = (p-1) * (q-1) berechnen.

Beispiel (Aufgabe 1): p = 5 und q = 13 -> φ(n) = 48

Mr(s). X weiß zudem, dass die Zahl d modulares Inverses von e bzgl. φ(n) ist bzw., dass [e*d]%φ(n) = 1 gilt. Mit dem erweiterten euklidischen Algorithmus kann Mr(s). X diese Zahl d bestimmen.

Beispiel (Aufgabe 1): e = 19 und φ(n) = 48: [19*d]%48 = 1 -> d = 43

Mr(s). X kennt jetzt den privaten Schlüssel und kann den Geheimtext entschlüsseln.

Sicherheit des RSA-Verfahrens

Die Sicherheit beruht darauf, ob Mr(s). X aus dem öffentlichen Schlüssel (e, n) den privaten Schlüssel (d, n) berechnen kann.

Wie oben gezeigt wurde, ist das immer möglich. Wieso soll dann das RSA-Verfahren sicher sein? Die Sicherheit beruht letztlich darauf, ob diese Berechnung in akzeptabler Zeit durchführbar ist.

Die Schwierigkeit bei der Berechnung des privaten Schlüssels besteht darin, die Zahl n in ein Produkt p*q aus Primzahlen zu zerlegen.

Prinzipiell ist eine solche Zerlegung immer möglich. Probleme ergeben sich, wenn die Primzahlen sehr groß sind. Die Zerlegung dauert dann unter Umständen so lange, dass es praktisch unmöglich ist, den privaten Schlüssel zu bestimmen.

Im nächsten Abschnitt werden wir uns mit dieser Problematik ausführlicher beschäftigen.