Automatisierung der Berechnungen
Simulation mit einem Surfmodell
Wir gehen weiterhin von der folgenden Webseitenwelt aus:
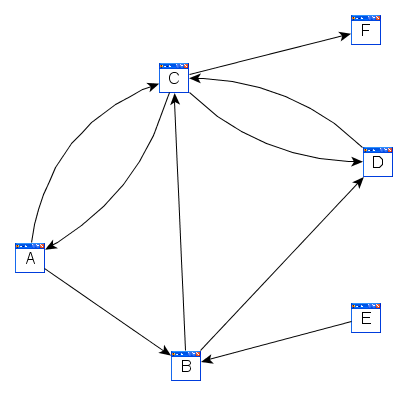
Wir machen folgende Annahmen zum Surfverhalten von Nutzern:
(A1) Zu Beginn wird jede Webseite von einer bestimmten Anzahl von Nutzern besucht. Wir bezeichnen die Anzahlen mit a, b, c, d, e und f (im Beispiel: 300).
(A2) Gelegenheitsjumper: Ein bestimmter Prozentsatz der Nutzer (im Beispiel: 20%) springt in jedem Takt zu einer beliebigen Webseite. Sie teilen sich dabei gleichmäßig auf alle zur Verfügung stehenden Webseiten auf.
(A3) Surfer: Alle anderen Besucher (im Beispiel: 80%) folgen im gleichen Takt einem Link auf eine weitere Webseite. Wenn auf einer Webseite mehrere Links vorkommen, dann verteilen sich die Besucher gleichmäßig auf die verschiedenen Links.
(A4) Sackgassenjumper: Besucher, die in eine Sackgasse geraten (d.h. Webseiten besuchen, die keine Links auf weitere Seiten enthalten), besuchen im nächsten Schritt irgend eine der gegebenen Webseiten. Sie teilen sich dabei gleichmäßig auf alle zur Verfügung stehenden Webseiten auf.
Aufgabe 1
(a) Erkläre mit den Annahmen die Berechnungsausdrücke in der folgenden Abbildung. Was beschreiben sie?
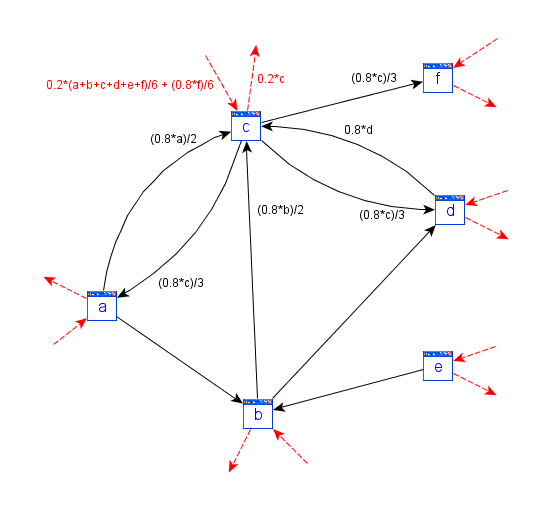
(b) Ergänze entsprechende Berechnungsausdrücke an den weiteren Pfeilen.
Berechnungen mit Python
Die Berechnungen zum Surfverhalten einer großen Anzahl von Nutzern sollen jetzt automatisiert durchgeführt werden. Bearbeite hierzu die folgenden Aufgaben.
Aufgabe 2
Wir beginnen mit dem folgenden Python-Programm:
a = 300
b = 300
c = 300
d = 300
e = 300
f = 300
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
(a) Analysiere zunächst das Programm. Versuche, die Bedeutung von jeder Programmzeile zu erklären. Beachte, dass das Backslashsymbol "\" in Python benutzt wird, um Zeilen zu verbinden. Hier einige zu klärende Fragen:
-
Welche Daten werden am Anfang mit den Variablen
a,b,c,d,e,fverwaltet? -
Wozu werden die Variablen
a_neu,b_neu,c_neu,d_neu,e_neu,f_neubenutzt? -
Was leistet die Zuweisung
a = 300? -
Was leistet die Zuweisung
a_neu = (0.8*c)/3 + (0.2*(a+b+c+d+e+f))/6 + (0.8*f)/6? - Was leistet das gesamte Programm?
(b) Lass das Programm von Python ausführen. Vergleiche die ausgegebenen Ergebnisse mit den selbst berechneten.
Aufgabe 3
Jetzt soll ein weiterer Simulationsschritt hinzukommen:
Ein erster Vorschlag für ein erweitertes Programm könnte so aussehen:
a = 300
b = 300
c = 300
d = 300
e = 300
f = 300
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
(a) Teste dieses Programm. Was fällt auf? Können die ausgegebenen Ergebnisse alle stimmen?
(b) Irgendetwas stimmt in dem Programm nicht. Hast du schon eine Vermutung, warum das Programm nicht die beabsichtigten Ergebnisse liefert?
(c) Ergänze im Programm weitere print-Anweisungen (s.u.). Ist jetzt alles klar?
a = 300
b = 300
c = 300
d = 300
e = 300
f = 300
print(a, b, c, d, e, f)
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
Aufgabe 4
Zur Behebung der Schwierigkeiten werden weitere Zuweisungen im Programm ergänzt.
a = 300
b = 300
c = 300
d = 300
e = 300
f = 300
print(a, b, c, d, e, f)
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
a = a_neu
b = b_neu
c = c_neu
d = d_neu
e = e_neu
f = f_neu
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
a = a_neu
b = b_neu
c = c_neu
d = d_neu
e = e_neu
f = f_neu
print(a, b, c, d, e, f)
print(a_neu, b_neu, c_neu, d_neu, e_neu, f_neu)
(a) Teste auch dieses Programm. Jetzt sollten die ausgegebenen Ergebnisse stimmen.
(b) Kannst du erklären, was die hinzugefügten Zuweisungen (wie z.B. a = a_neu)
hier bewirken?
Aufgabe 5
Die Ausgabe der jeweiligen Besucherzahlen soll etwas verbessert werden. Hierzu soll eine Art Schrittzähler eingeführt werden.
zaehler = 0
a = 300
b = 300
c = 300
d = 300
e = 300
f = 300
print(zaehler)
print(a, b, c, d, e, f)
print()
zaehler = zaehler + 1
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
a = a_neu
b = b_neu
c = c_neu
d = d_neu
e = e_neu
f = f_neu
print(zaehler)
print(a, b, c, d, e, f)
print()
zaehler = zaehler + 1
a_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
b_neu = (0.8*a)/2 + (0.8*e) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
c_neu = (0.8*a)/2 + (0.8*b)/2 + (0.8*d) + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
d_neu = (0.8*c)/3 + (0.8*b)/2 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
e_neu = 0 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
f_neu = (0.8*c)/3 + \
(0.2*(a+b+c+d+e+f))/6 + \
(0.8*f)/6
a = a_neu
b = b_neu
c = c_neu
d = d_neu
e = e_neu
f = f_neu
print(zaehler)
print(a, b, c, d, e, f)
print()
(a) Analysiere zunächst das gezeigte Programm. Stelle Vermutungen auf, was das Programm leistet.
(b) Überprüfe deine Vermutungen, indem du das Programm von Python ausführen lässt.
(c) Kannst du die Wirkung der Zuweisung zaehler = zaehler + 1 erklären?
(d) Wie kann man das Programm weiter ergänzen, um die Ergebnisse von 4 Simulationsschritten zu erhalten?
